
Xray diffraction analysis software#
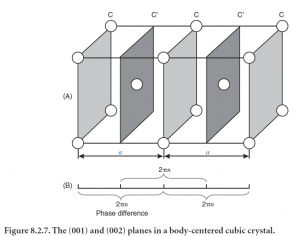
XRD analysis software can remove them with analytical functions).įigure 3: Three diffraction ray paths, of which rays 11' and 22' satisfy the Bragg condition, while ray 33' results from scattering by an atom (red circle) at an arbitrary position.Īs the only factor that carries the unique structural contribution of a material to the relative intensities of XRD peaks, the structure factor is very important and requires a closer look. The remaining factors, the 'multiplicity', which accounts for all the planes that belong to the same family because they are symmetrically related, and the 'Lorentz-Polarization' factor, which comes from the geometry of the XRD experiment, also affect the relative intensity of the peaks but they are not specific to a material and can easily be accounted for with analytical expressions (i.e. The 'structure factor' directly affects the intensity of specific peaks as a direct result of the structure. In other words, the contribution by the absorption factor to the intensity of different peaks is constant. We can typically assume n=1, and, in general, n=1 for θ 3 times thicker than the attenuation length of the X-rays). At n=1, for example, we have the first harmonic, meaning that the path of X-rays diffracted through the crystal (equivalent to 2d hkl sin ) is exactly 1 λ, while at n=2, the diffracted path is 2 λ. Finally, n is an integer that represents the 'harmonic order' of the diffraction. Here λ is the wavelength of the X-rays used, d hkl is the spacing between a particular set of planes with (hkl) Miller indices*, and θ is the angle of incidence at which a diffraction peak is measured. Bragg identified the relationship illustrated in Figure 1 and derived a corresponding equation: At certain angles of incidence, the diffracted parallel waves constructively interfere and create detectable peaks in intensity. When light waves of sufficiently small wavelength are incident upon a crystal lattice, they diffract from the lattice points. Relationship between diffracted peak positions and crystal structure: WAXD covers an angular range beyond 10 0. SAXS measures structural correlations of the scale of several nanometers or larger (such as crystal superstructures), and X-ray reflectivity that measures the thickness, roughness, and density of thin films. Other elastic scattering based X-ray techniques include small angle X-ray scattering (SAXS), where the X-rays are incident on the sample over the small angular range of 0.1-10 0 typically). XRD, which is generally used to mean can wide-angle X-ray diffraction (WAXD), falls under several methods that use the elastically scattered X-ray waves.
The diffraction of the X-rays, that is central to the XRD method, is a subset of the general X-ray scattering phenomena. Beyond being able to measure the average positions of the atoms in the crystal, information on how the actual structure deviates from the ideal one, resulting for example from internal stress or from defects, can be determined. The intensity of the scattered X-rays are plotted as a function of the scattering angle, and the structure of the material is determined from the analysis of the location, in angle, and the intensities of scattered intensity peaks. This is done by irradiating a sample of the material with incident X-rays and then measuring the intensities and scattering angles of the X-rays that are scattered by the material. X-ray diffraction (XRD) is a technique used in materials science for determining the atomic and molecular structure of a material.
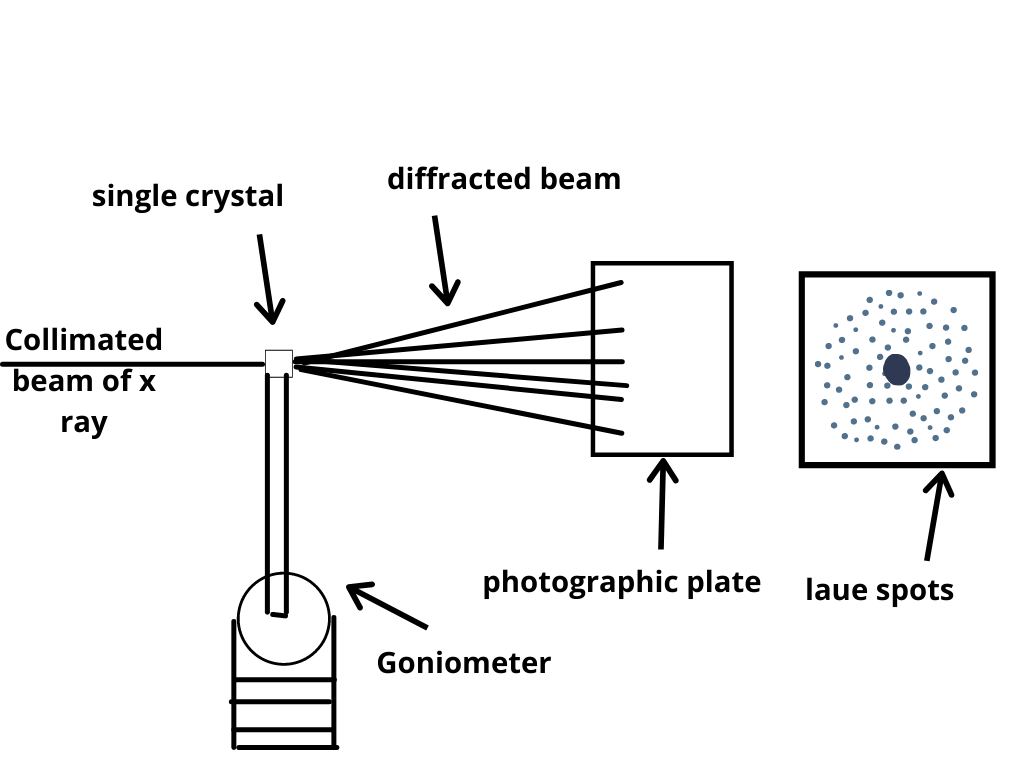
Source: Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA


 0 kommentar(er)
0 kommentar(er)
